Since 2000

The Tetrabrot

A 3D generalization of the Mandelbrot set, discovered by Dominic Rochon in 2000 — the first 3D slice of the tricomplex Multibrot set.

In multicomplex dynamics, the Tetrabrot is a 3D generalization of the Mandelbrot set^[1]. Discovered by Dominic Rochon in 2000, it can be interpreted as a 3D slice ${\mathcal {T}}^{2}(1,\mathbf {i_{1}} ,\mathbf {i_{2}} )$ of the tricomplex Multibrot set ${\mathcal {M}}_{3}^{2}$ ^[2].

Illustration of filled-in Julia sets related to the Tetrabrot

1 Divergence-layers algorithm
2 Generalized Fatou-Julia theorem
3 Ray-tracing
4 Conjecture
5 See also
6 References
7 External links

Divergence-layers algorithm

There are different algorithms to generate pictures of the Tetrabrot. In the tricomplex space^[11], the algorithms use the tricomplex function $f_{c}(\eta ):=\eta ^{p}+c$ where $\eta$ , $c\in \mathbb {TC}$ and $p\geq 2$ is an integer. Since $c\in {\mathcal {T}}^{2}(1,\mathbf {i_{1}} ,\mathbf {i_{2}} )$ if and only if $|f_{c}^{m}(0)|\leq 2\,\,\forall m\geq 1$ . For a given number of iterations $M$ , if the computations of $f_{c}^{m}(0)$ for $m\in \left\lbrace 1,2,\ldots ,M\right\rbrace$ is $|f_{c}^{m}(0)|>2$ a level surface can be associated to this integer. In this way, it is possible to draw a different level surface associated to different integers. This is called the Divergence-Layer Algorithm. It is used to draw the Tetrabrot in the 3D space.

Illustration of the Tetrabrot with the Divergence-Layer Algorithm

Generalized Fatou-Julia theorem

The tricomplex filled-in Julia set of order $p=2$ for $c\in \mathbb {TC}$ is defined as

${\mathcal {K}}_{3,c}^{2}:=\left\lbrace \eta \in \mathbb {TC} \,:\,\left\lbrace f_{c}^{m}(\eta )\right\rbrace _{m=1}^{\infty }{\text{ is bounded}}\right\rbrace .$

The basin of attraction at $\infty$ of $f_{c}(\eta )=\eta ^{2}+c$ is defined as $A_{3,c}(\infty ):=\mathbb {TC} \smallsetminus {\mathcal {K}}_{3,c}^{2}$ , that is

$A_{3,c}(\infty )=\left\lbrace \eta \in \mathbb {TC} \,:\,f_{c}(\eta )\rightarrow \infty {\text{ as }}\eta \rightarrow \infty \right\rbrace$

and the strong basin of attraction of $\infty$ of $f_{c}$ as

$SA_{3,c}(\infty ):=\left[A_{c_{\gamma _{1}\gamma _{3}}}(\infty )\times _{\gamma _{1}}A_{c_{{\overline {\gamma _{1}}}\gamma _{3}}}(\infty )\right]\times _{\gamma _{3}}\left[A_{c_{\gamma _{1}{\overline {\gamma _{3}}}}}(\infty )\times _{\gamma _{1}}A_{c_{{\overline {\gamma _{1}}}{\overline {\gamma _{3}}}}}(\infty )\right]$ where $A_{c}(\infty )$ is the basin of attraction of $f_{c}$ at $\infty$ for $c\in \mathbb {C} (\mathbf {i_{1}} )$ .

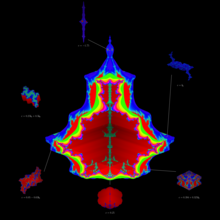
Illustration of the Fatou-Julia theorem for the Tetrabrot

With these notations, the generalized Fatou-Julia theorem for ${\mathcal {M}}_{3}^{2}$ is expressed in the following way^[2]^[3]:

$0\in {\mathcal {K}}_{3,c}^{2}$ if and only if ${\mathcal {K}}_{3,c}^{2}$ is connected;
$0\in SA_{3,c}(\infty )$ if and only if ${\mathcal {K}}_{3,c}^{2}$ is a Cantor set;
$0\in A_{3,c}(\infty )\smallsetminus SA_{3,c}(\infty )$ if and only if ${\mathcal {K}}_{3,c}^{2}$ is disconnected but not totally.

In particular, ${\mathcal {K}}_{3,c}^{2}$ is connected if and only if $c\in {\mathcal {M}}_{3}^{2}$ . For each statements, a specific color can be assigned to a specific case to obtain some information on the topology of the set.

Ray-tracing

In 1982, A. Norton^[4] gave some algorithms for the generation and display of fractal shapes in 3D. For the first time, iteration with quaternions^[5] appeared. Theoretical results have been treated for the quaternionic Mandelbrot set^[6] ^[7] (see video) defined with quadratic polynomial in the quaternions of the form $q^{2}+c$ .

Quaternion Julia set with parameters c = 0.123 + 0.745i and with a cross-section in the XY plane. The "Douady Rabbit" Julia set is visible in the cross section

In 2005, using bicomplex numbers, É. Martineau^[8] and D. Rochon^[9] obtained estimates for the lower and upper bounds of the distance from a point $c$ outside of the bicomplex Mandelbrot set ${\mathcal {M}}_{2}^{2}$ to ${\mathcal {M}}_{2}^{2}$ itself. Let $c\not \in {\mathcal {M}}_{2}^{2}$ and define

d(c,{\mathcal {M}}_{2}^{2}):=\inf \left\lbrace |w-c|\,:\,w\in {\mathcal {M}}_{2}^{2}\right\rbrace .

Then,

d(c,{\mathcal {M}}_{2}^{2})={\sqrt {\frac {d(c_{\gamma _{1}},{\mathcal {M}}^{2})+d(c_{\overline {\gamma _{1}}},{\mathcal {M}}^{2})}{2}}}

where ${\mathcal {M}}^{2}$ is the standard Mandelbrot set.

The Mandelbrot set

{\mathcal {M}}^{2}

with continuously colored environment

Using the Green function $G:\mathbb {C} (\mathbf {i_{1}} )\smallsetminus {\mathcal {M}}^{2}\rightarrow \mathbb {C} (\mathbf {i_{1}} )\smallsetminus {\overline {B_{1}}}(0,1)$ in the complex plane, where ${\overline {B_{1}}}(0,1)$ is the closed unit ball of $\mathbb {C} (\mathbf {i_{1}} )\simeq \mathbb {C}$ , the distance is approximated in the following way^[10]

{\frac {|z_{m}|\ln |z_{m}|}{2|z_{m}|^{1/2^{m}}|z_{m}'|}}\approx {\frac {\sinh G(c_{\gamma })}{2^{G(c_{\gamma })}|G'(c_{\gamma })|}}<d(c_{\gamma },{\mathcal {M}}^{2})

$\forall c_{\gamma }\in \mathbb {C} (\mathbf {i_{1}} )\smallsetminus {\mathcal {M}}^{2}$ and for large $m$ where $z_{m}:=f_{c_{\gamma }}^{m}(0)$ and $z_{m}':=\left.{\frac {d}{dc}}f_{c}(0)\right|_{c=c_{\gamma }}$ . This approximation gives a lower bound that can be used to ray-trace the Tetrabrot.

Tetrabrot ray-traced

There exist also a generalization of the lower bound for $d(c,{\mathcal {M}}_{2}^{2})$ to the tricomplex Multibrot set of order $p$ ^[11]. Some ressources and images can be found on the Aleph One's personal page^[12]. There is also a video available on Youtube where specific regions of the Rochon's Tetrabrot are explored.

References

^ ^a ^b D. Rochon, "A Generalized Mandelbrot Set for Bicomplex Numbers", Fractals, 8(4):355-368, 2000. doi:10.1142/S0218348X0000041X
^ ^a ^b V. Garrant-Pelletier and D. Rochon, "On a Generalized Fatou-Julia Theorem in Multicomplex Space", Fractals, 17(3):241-255, 2008. doi:10.1142/S0218348X03002075
^ V. Garant-Pelleter, Ensemble de Mandlebrot et de Julia remplis classiques généralisés aux espaces multicomplexes et théorème de Fatou-Julia généralisé, Master's thesis, Université du Québec à Trois-Rivières, 2011.
^ A. Norton, "Generation and Display of Geometric Fractals in 3-D", Computer Graphics, 16:61-67, 1982. doi:10.1145/965145.801263
^ I. L. Kantor, Hypercomplex Numbers, Springer-Verlag, New-York, 1982.
^ S. Bedding and K. Briggs, "Iteration of Quaternion Maps", Int. J. Bifur. Chaos Appl. Sci. Eng., 5:877-881, 1995. doi:10.1142/S0218127495000661
^ J. Gomatam, J. Doyle, B. Steves and I. McFarlane, "Generalization of the Mandelbrot Set: Quaternionic Quadratic Maps", Chaos, Solitons & Fractals, 5:971-985, 1995. doi:10.1142/S0218127495000661
^ É. Martineau, Bornes de la distance � l'ensemble de Mandelbrot généralisé, Master's thesis, Université du Québec à Trois-Rivières, 2004.
^ É. Martineau and D. Rochon, "On a Bicomplex Distance Estimation for the Tetrabrot", International Journal of Bifurcation and Chaos, 15(6):501-521, 2005. doi:10.1142/S0218127405013873
^ J. C. Hart, D. J. Sandin and L. H. Kauffman, "Ray tracing deterministic 3-D fractals", Comput. Graph., 23:289-296, 1989.
^ ^a ^b D. Rochon, "On a Tricomplex Distance Estimation for Generalized Multibrot Sets", CHAOS 2017. 3dfractals.com/docs/Chaos_2017.pdf
^ http://aleph1.sourceforge.net/gallery/mandelbrot/

The Tetrabrot

Contents

Divergence-layers algorithm

Generalized Fatou-Julia theorem

Ray-tracing

See also

References

External links