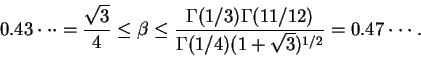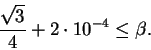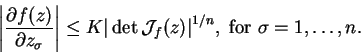Introduction

Since confirmation of the Bieberbach conjecture by de Branges, perhaps the outstanding open problem in complex analysis is that of finding the exact value of the Bloch constant.

Let $H(B)$ be the class of functions $w=f(z)$ holomorphic in the unit disc $B=\{z\in\mathbb {C}:\vert z\vert<1\}$. In 1925, Bloch [3] proved the famous theorem which bears his name:

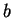
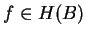
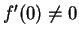
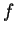
Theorem 1 (Bloch)   There exists a positive constant $b$ such that if $f\in H(B)$ and $f^\prime(0)\neq 0$, then $f$ maps some subdomain of B biholomorphically onto a disc of radius $b\cdot\vert f^\prime(0)\vert$.

Such a disc is called a univalent disc for $f$. The Bloch constant may be described as:

$$\beta=\mbox{inf}\{\beta_{f}:f\in H(B)\mbox{ with }f^\prime(0)=1\}$$

where $\beta_{f}=\mbox{sup}\{b: f(B)\mbox{ contains a univalent disc of radius b}\}$. In this paper, we introduce Bloch constants for other classes of mappings and find one which is precisely equal to the classical Bloch constant $\beta$.

The following upper and lower estimates for $\beta$ were found by Lars Ahlfors and Grunsky [2] and Ahlfors [1]:

$$0.43\cdot\cdot\cdot=\frac{\sqrt{3}}{4}\leq\beta\leq\frac{\Gam... ...a(11/12)} {\Gamma(1/4)(1+\sqrt{3})^{1/2}}=0.47\cdot\cdot\cdot.$$

It is conjectured that the correct value of $\beta$ is precisely this upper bound. Recently, on the basis of Bonk's work [5] and the Schwarz-Pick lemma, Chen Huaihui and P. M. Gauthier [6] improved the lower bound for Bloch's constant further as follows:

$$\frac{\sqrt{3}}{4}+2\cdot 10^{-4}\leq\beta.$$

Passing to several complex variables, a holomorphic mapping $f$ from a domain in $\mathbb {C}^{n}$ into $\mathbb {C}^{n}$ is said to be nondegenerate if $det\mathcal{J}_{f}$ is not identically zero on the domain. Let $B^{n}$ denote the open unit ball in $\mathbb {C}^{n}$. A nondegenerate mapping $f$ from $B^{n}$ into $\mathbb {C}^{n}$ is said to be normalized if $det\mathcal{J}_{f}(0)=1$, where $0$ denotes the origin in $\mathbb {C}^{n}$. For such $f$ we denote by $\beta_{f}$ the supremum of values $b$ such that the image $f(B^{n})$ contains a univalent ball of radius $b$. If we fix $K>0$ and consider the holomorphic mapping $f:\mathbb {C}^{2} \longrightarrow\mathbb {C}^{2}$ defined by

$$f(z_{1},z_{2})=(z_{1}/\sqrt{K},\sqrt{K}z_{2}),$$

then, $f$ is normalized but $\beta_{f}=1/\sqrt{K}$. Since $K$ can be chosen arbitrarily large, we see that there is no Bloch theorem for general holomorphic mappings, when $n>1$. One might argue that the correct generalization of the normalization $\lq\lq f^\prime(0)=1''$ to several variables is not $\lq\lq det \mathcal{J}_{f}(0)=1''$. However, there are also examples of holomorphic mappings $f$, with the stronger normalization $\mathcal{J}_{f}(0)=I$ ($I$ is the identity mapping) and for which $\beta_{f}$ is arbitrarily small. One of the results of this article is to show that in the case of $\mathbb {C}^{2}$ the stronger normalization is correct, if the mapping $f$ satisfies the complexified Cauchy-Riemann equations. Thus, we see that for $n>1$ we need to restrict the class of mappings to a more specific subclass to obtain a Bloch theorem. One of the well known subclasses is the class of $K$-quasiregular mappings. For $n\geq 1$, let $\vert$ $\vert$ denote the usual norm in $\mathbb {C}^{n}$.

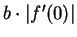
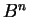
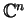
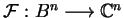
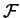
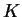
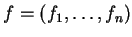
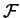
Definition 1 (Wu)   Let ${B}^{n}$ be the open unit ball of $\mathbb {C}^{n}$ and let $\mathcal{F}:{B}^{n}\longrightarrow\mathbb {C}^{n}$ be a family of holomorphic mappings. We say $\mathcal{F}$ is K-quasiregular iff there exists a constant $K$ so that, for each $f=(f_{1},\ldots,f_{n})$ of $\mathcal{F}$, the following holds throughout ${B}^{n}$,

$$\left\vert\frac{\partial{f(z)}}{\partial{z}_{\sigma}}\right... ...\mathcal{J}_{f}(z)\vert}^{1/n},\mbox{ for }\sigma=1,\ldots,n.$$

For such a class of mappings, it is possible to find a Bloch theorem in $\mathbb {C}^{n}$. Wu found a beautiful proof of this in [21]:

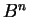
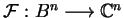
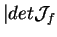
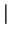
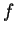
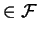
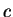
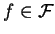
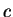
Theorem 2 (Wu, 1967)   Let $\mathcal{F}:{B}^{n}\longrightarrow\mathbb {C}^{n}$ be a K-quasiregular family of holomorphic mappings such that $\vert det \mathcal{J}_{f}$(0)$\vert$=1 for all $f$ $\in\mathcal{F}$. Then, there is a positive constant $c$ such that every $f\in\mathcal{F}$ possesses a univalent ball of radius $c$.

As Wu pointed out, this result also follows from the work of Bochner [4] in 1946. It is possible to find lower estimates for the Bloch constant for this class of mappings in [7], [17] and [20] provided we adapt correctly the definitions. We note also that the estimates depend on the $K$ of quasiregularity.

In this article, we use a generalization of complex numbers called bicomplex numbers ([13], [16], [14]) to find another subclass of mappings which has a Bloch constant in $\mathbb {C}^{2}$. Moreover, we find the estimates: $\frac{\beta}{\sqrt{2}}\leq\delta\leq\sqrt{2}\beta$ for this Bloch constant $\delta$, whenever our mappings are on the unit ball, and we find a specific domain of $\mathbb {C}^{2}$ where the Bloch constant has the same value as the Bloch constant for one variable. Finally we show that this class of mappings does not depend on the quasiregularity.