Example 1
Let
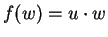
, where
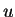
and
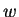
are in
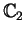
. If
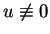
is noninvertible then, f is not quasiregular. If
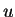
is
invertible, then
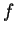
is
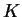
-quasiregular for
where
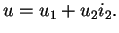
In particular, if
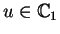
, then
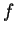
is conformal. However, we note in this example, that
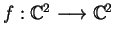
is a linear transformation which is nondegenerate if and only if
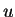
is invertible.
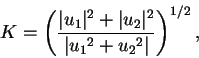
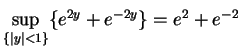 and then
and then
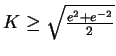 , i.e.
, i.e.
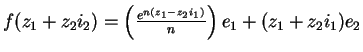 ,
then
,
then 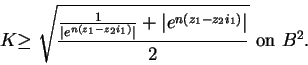
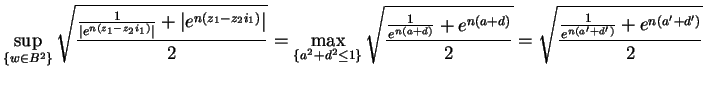 , where
, where
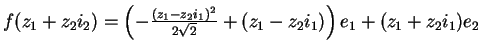 then
then